로지스틱 회귀란?
로지스틱 회귀(Logistic Regression)는 회귀를 사용하여 데이터가 어떠한 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘입니다.
어떠한 범주에 속할 확률을 0에서 1 사이의 값으로 예측하기 때문에 주로 이항형 문제(즉, 유효한 범주의 개수가 두개인 경우)를 지칭할 때 사용됩니다.
Ex) 스팸 메일 분류
메일을 받았을 때 그것이 스팸일 확률이 0.5 이상이면 spam으로 분류하고, 확률이 0.5보다 작은 경우 ham으로 분류하는 것
위의 상황처럼 데이터가 2개의 범주 중 하나에 속하도록 결정하는 것을 2진 분류(binary classification)라고 합니다.
Pass or Fail 강의가 있다고 가정하고 시험 공부시간에 따른 Pass / Fail 여부를 예측하는 Binary Classification모델을 구성해보자.
 Pass/Fail에 따른 0, 1 encoding
Pass/Fail에 따른 0, 1 encoding
공부 시간에 따른 패논패 여부를 2차원 그래프에 나타내면 다음과 같습니다.

이러한 상관관계를 예측하기위해 선형회귀를 사용한다면 다음과 같습니다.

보시는 것과 같이 선형회귀를 사용했을 때는 pass fail 여부를 올바르게 예측하지 못하고있습니다.
만약 1차 함수로 나타낸다면 다음과 같은 모양이 그나마 적합할수 있겠습니다.

이러한 문제를 해결하기 위해서 시그모이드 함수를 사용합니다.
시그모이드 함수란 무한대의 실수 값을 0과 1 사이의 확률 값으로 변환하는 역할을 합니다.
입력 값의 절대 값이 커질수록 기울기가 0으로 수렴하는 단점이 있습니다.
시그모이드 함수를 파이썬으로 구현해보면 다음과 같습니다.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.plot([0,0],[1.0,0.0], ':')
plt.title("Sigmoid")
plt.show()

아래 코드는 시험공부시간에 따른 패논패 여부를 예측하는 모델의 코드입니다.
import torch
import torch.optim as optim
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
device = 'cuda' if torch.cuda.is_available() else 'cpu'
x = torch.tensor([[1.5], #시험 공부 시간
[2],
[4.5],
[7],
[5.4],
[10],
[12],
[6],
[8],
[9.7]]).to(device)
y = torch.tensor([0,0,0,1,0,1,1,0,1,1], #pass/fail 여부 fail(0), pass(1)
dtype = torch.float32)
y = y.reshape((len(y),1)).to(device)
class ClassficationModel(nn.Module):
def __init__(self):
super().__init__()
self.fn1 = nn.Linear(1, 3)
self.fn2 = nn.Linear(3, 3)
self.fn3 = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
self.relu = nn.ReLU() #역전파에서 Gradient vanishing effect를 해결하기 위해 ReLU 함수 사용
def forward(self, x):
y1 = self.relu(self.fn1(x))
y2 = self.relu(self.fn2(y1))
y = self.fn3(y2)
return self.sigmoid(y)
model = ClassficationModel()
model.to(device)
learning_rate = 1e-2
optimizer = optim.SGD(model.parameters(),
learning_rate)
loss = nn.BCELoss()
COST = np.zeros(100000)
for i in range(100000) :
prediction = model(x)
cost = loss(prediction, y)
optimizer.zero_grad()
cost.backward()
optimizer.step()
COST[i]= cost.item()
print(f'Step : {i}, mse : {cost.item()}')
X_test = torch.arange(1, 13, dtype = torch.float32)
X_test = X_test.reshape((len(X_test),1))
plt.plot(COST)
plt.show()
plt.plot(x, y, 'x')
plt.plot(X_test, model(X_test).detach())
plt.show()
출력
 Cost
Cost
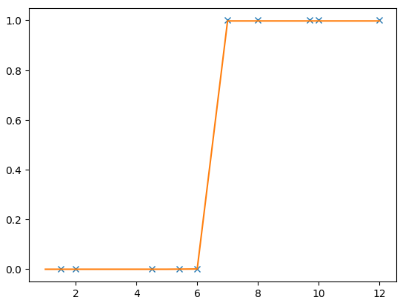 결과
결과
위의 그래프를 보면 공부시간에 따른 패논패 여부를 예측한 그래프가 올바르게 피팅되어있는 모습을 볼 수 있다. (성공)










